本コラムでは、これから許容応力度計算を始めたい方、力学に対する理解を深めたい方に向けて
専門的な知識をより分かりやすく解説し、業務に役立つ情報を提供できればと考えております。
メルマガを購読されているユーザー様へは、HP公開よりいち早くお届けしますのでぜひご登録ください!
●力とは何か
材料と断面の性質の理解に不可欠な、「力とは何か」から話を始めたいと思います。
まず、力は「大きさと向き」を持つベクトル量です。
大きさと向きを持つベクトルは、大きさのみを持つスカラとは物理的な意味が異なります。
構造に関係する図書や書籍を読むと、矢印(向き)が多く登場する理由もこの点が関係しています。
数値(または矢印の長さ)がベクトルの大きさ、矢印がベクトルの向きを表しています。
まさに、定義そのものです。
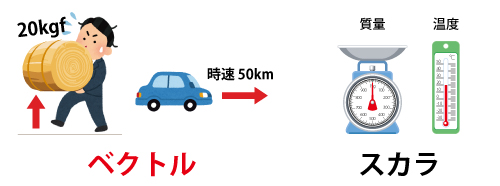
ベクトルとスカラの例を挙げると次のようなものがあります。
ベクトルの例:力、圧力、変位、速度、加速度など
・米俵を20kgfの力で持ち上げると、「数値的な大きさ」と”持ち上げるのに加えた上向きの力”という「向き」があります。
・車を時速50kmで走行すると、「数値的な大きさ」と”東に向かって走行”という「向き」があります。
スカラの例 :質量、面積、温度、身長、株価など
・面積は大きさを持ちますが、面積に向きの概念や情報はありません。
向きの概念や情報がないと言うより、面積を表現するのに向きは必要ありません。
また、ベクトルとスカラでは四則演算の方法も異なります。ベクトルの演算方法を理解しておくと、力をあつかう分野の
「なぜ」の解決に役立つことが少なくないので、忘れてしまった方はこれを機に復習してみてはいかがでしょうか。
●力の大きさとは
それでは、最初に力の大きさについて考えてみましょう。
力の大きさ(N:ニュートン、kN:キロニュートン)は、質量と加速度の掛け算で表されます。
物理の授業で聞いたことがある方も多いと思いますが、いわゆるニュートンの第二法則です。
![]()
力の大きさを数式で書くと、F=ma です。ここで、「F」は力、「m」は質量、「a」は加速度を表します。
ところで、「質量と重量の違い」、「変位と速度と加速度の関係」をご存知でしょうか。
簡単に言うと、質量と重量の違いは”重力”が関係しているか否かです。
地球で量った体重と月で量った体重は違うという話を聞いたことはありませんか?
地球と月では重力が異なるため、月で量ったときの体重は地球で量ったときの6分の1になります。
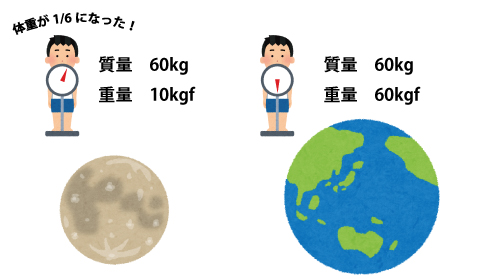
質量とは:不変的な物体そのものの量
重量とは:物体に働く重力の量
続いて、変位と速度と加速度の関係です。
<変位>
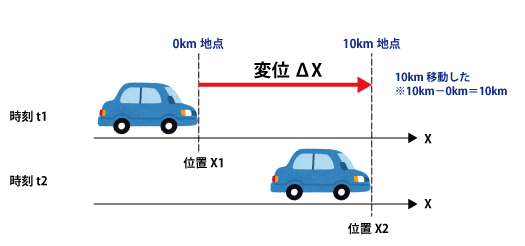
<速度>
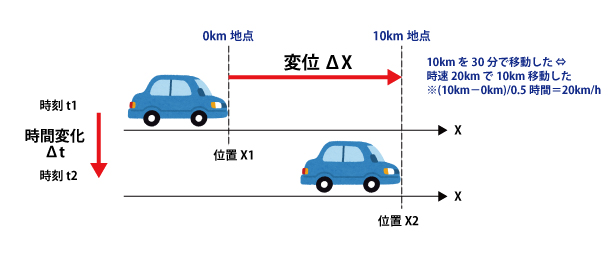
<加速度>
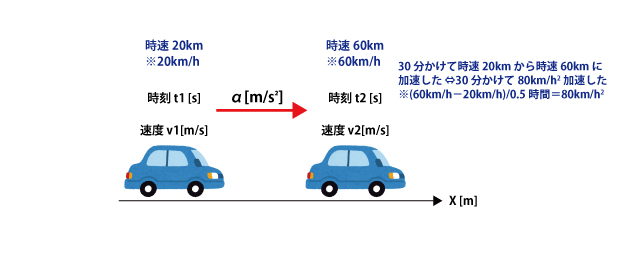
変位:距離、変形
速度:変位の変化率(生活に馴染んだ速度に車やバイクなどの時速km/hがあります)
加速度:速度の変化率(加速度的な成長など比喩表現としてよく聞くワードです)
私たちは、生活の中で加速度と力に関係があることを知っています。
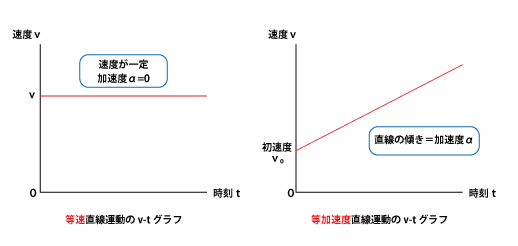
例えば、車で高速道路を時速80km/hで安定的に走っているとすると、このとき車は等速度運動をしています。
速度を変化させず一定の時速で車を走らせているため、座席に座っている人は力を感じません。このとき、加速度はゼロです。
しかし、時速80km/hから急激に速度を100km/hに加速したり、60km/hに減速したりすると、加速が生じるので体に力を感じます。
加速度は速度の変化率なので、緩やかに時速80km/hから100km/hに加速すると力は感じにくく、急激に時速80km/hから100km/hに
加速するとはっきりと力を感じます。

●力の単位
つぎに、力の単位を考えてみましょう。
実務で力を扱う場合、ニュートンやキロニュートンなどの単位が登場しますが、普段の生活ではキログラムやトンの方が一般的です。
同じ力を表しているのに、何が違うのでしょうか。
力の求め方はどちらも同じです(ニュートンの第二法則)。違うのは定義です。
普段の生活で扱う力の単位キログラムの定義
1kgf=1kg ✕ 9.8 \(m/s^2\)(=質量 ✕ 重力加速度)
計算などの実務で扱う力の単位ニュートンの定義
1N =1kg ✕ 1 \(m/s^2\)(=質量 ✕ 加速度)
体重や米俵の重さでよく使う(生活でよく登場する)キログラムは、重力加速度9.8 \(m/s^2\)が反映された大きさです。
これに対して実務で扱うニュートンは、質量1kgのモノに1 \(m/s^2\)の加速度を与えたときの力です。
したがって、両者には次の関係があります。
1N=1/9.8kgf → 9.8N=1kgf
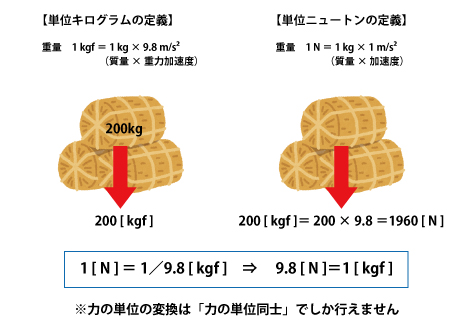
例えば、200kgfをニュートンに変換するには9.8を掛ければよいので、200✕9.8=1960N(1.96kN)です。
この値は、壁倍率1.0倍で登場する200kgf/mを1.96kN/mと表現する場合の計算と同じです。

力は、直接的な意味合いで使われる場合以外にも、「ストレスを感じる」や「威圧を感じる」に代表されるような
比喩表現としても多用されるほど生活に馴染んだ言葉ですが、よく考えてみると空気のようにそのものを見たことがありません。
なんとなく、体重計やパンチングマシーンなどで力を見ている気がしますが、体重計やパンチングマシーンは
見えない力を数値で可視化している道具なので、力そのものが見えているわけではありません。
お米や荷物を持ったときに力を見ている気がしますが、実際には力を感じているだけで見えてはいません。
地震や台風も、その力そのものも見ることができないので、受けた被害の大きさでその度合を測っていることに気付きます。
そう考えると、構造力学を難しく感じるのは見えないものを見ようとしているからかもしれません。
”見えないものを見ようとしている”ということを意識しながら力を考えると、教科書や参考書が不思議な表現や考え方を
している理由(気持ち)も理解できるのかもしれません。